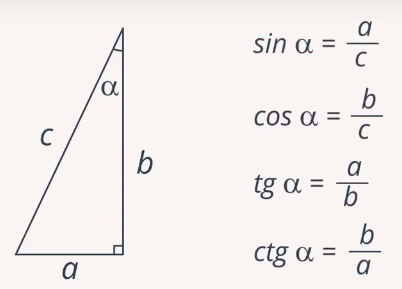Угол в прямоугольном треугольнике это отношение чего
Синус, косинус, тангенс и котангенс: определения в тригонометрии, примеры, формулы
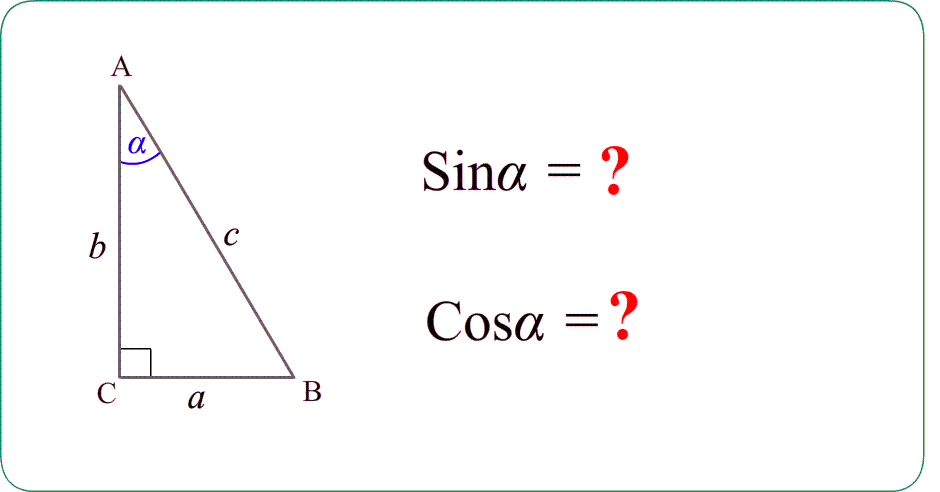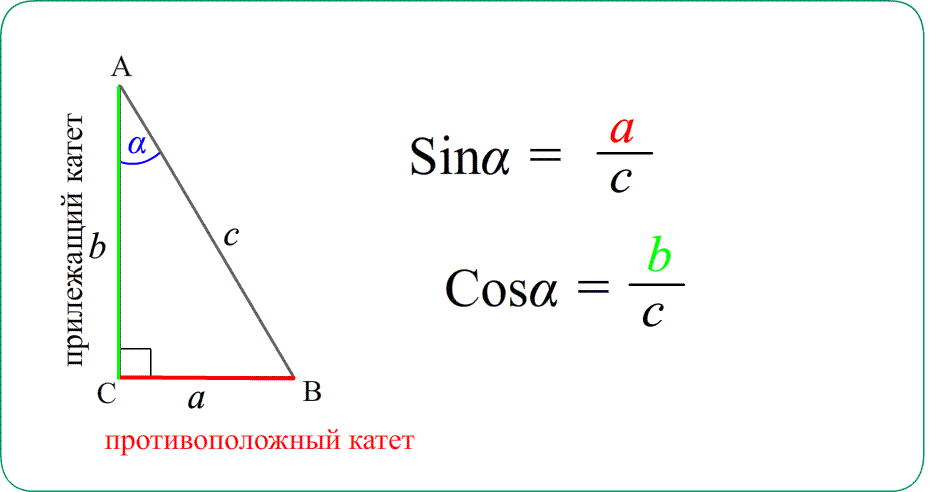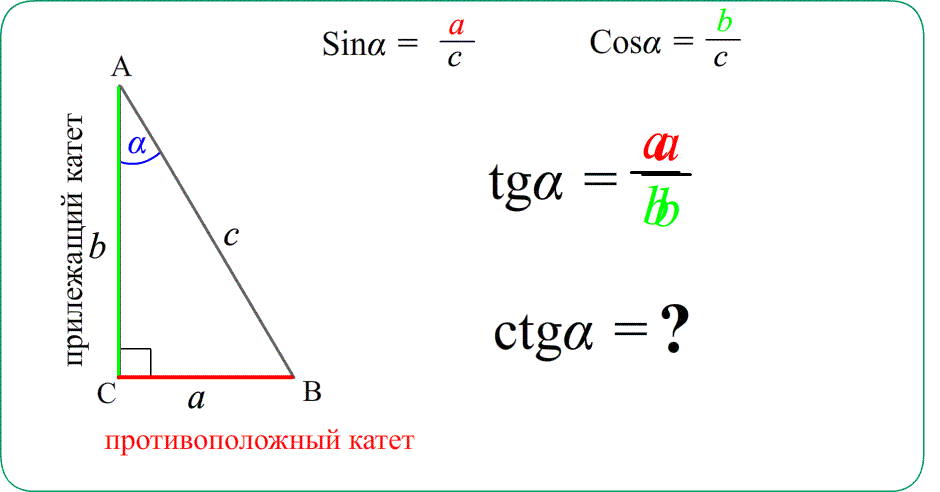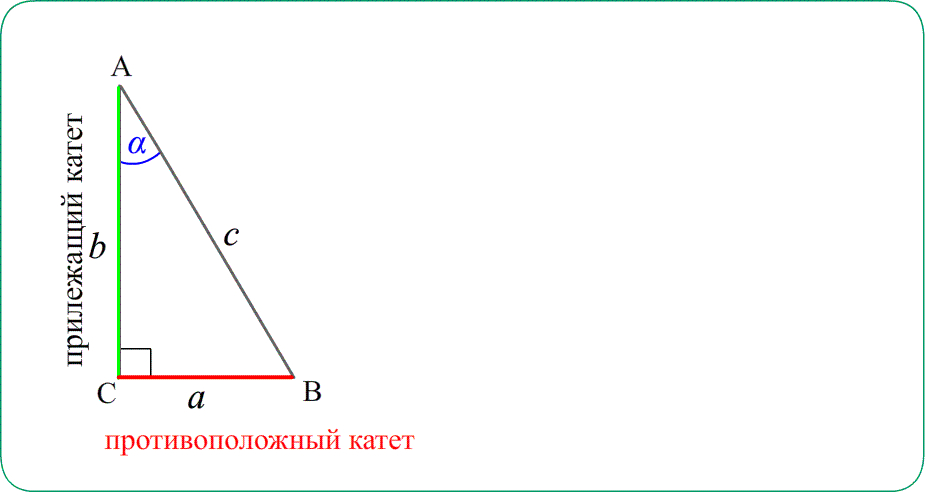
Рассмотрим еще одну задачу, которая может выйти как в первую часть, так и во вторую часть экзамена. Для решения повторим определения синусов и косинусов острых углов прямоугольного треугольника. Остается теперь только запомнить эти отношения:. Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе.
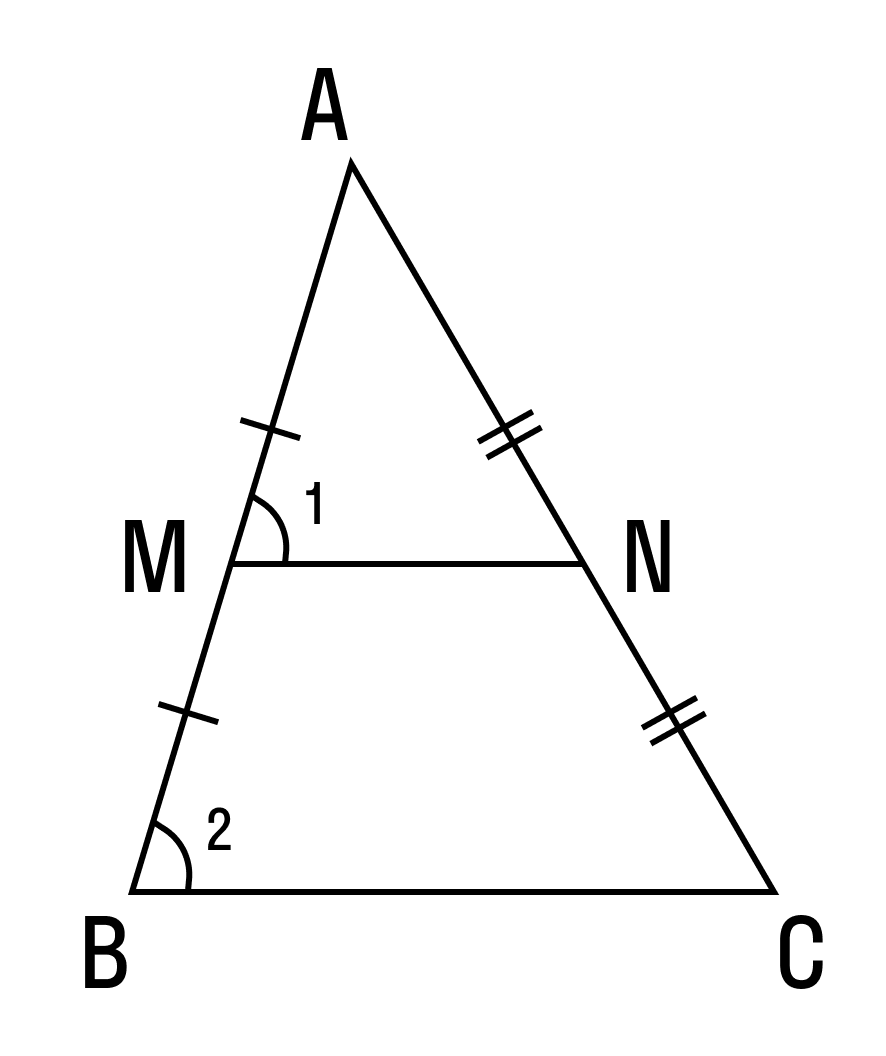
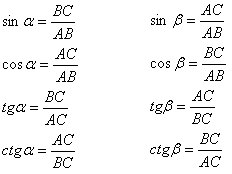


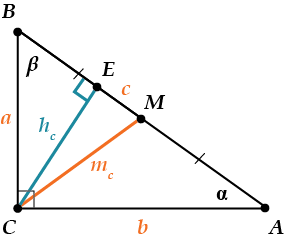


Синусы и косинусы в ОГЭ
Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии. Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.
- Как это всё запомнить?
- Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.
- Презентация и конспект урока по геометрии в 8 классе по теме «Соотношение между сторонами и углами в прямоугольном треугольнике».
- Чтобы войти в систему и использовать все возможности "Академии Хана", пожалуйста, включите JavaScript в своём браузере. Внести пожертвование Войти Зарегистрироваться Поиск курсов, уроков и видеороликов.
- Тригонометрические функции произвольных углов.
- Нарисуем прямоугольный треугольник , угол прямой.
- В данной статье мы познакомимся с разделом математики, история которого уходит в глубокую древность: времена Вавилона, Древнего Китая, Древнего Египта, Древней Греции.
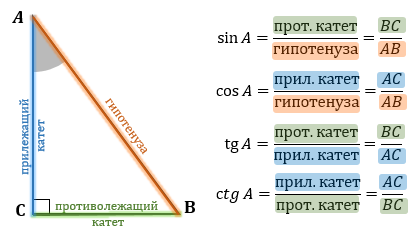
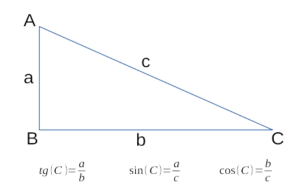
- Синус, косинус и тангенс острого угла прямоугольного треугольника. Сейчас рассмотрим что же такое синус, косинус, тангенс и котангенс в прямоугольном треугольнике?
- Синус, косинус, тангенс, котангенс — коротко о главном.
- Соотношения между сторонами и углами прямоугольного треугольника лежат в основе тригонометрии. Если высота проведена к гипотенузе, то треугольник делится на два меньших треугольника, подобных исходному и подобных друг другу.
- Синусом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к гипотенузе.
- Формирование у обучающихся понятий синуса, косинуса, тангенса и котангенса острого угла прямоугольного треугольника посредством организации обучающей деятельности по усвоению определений;.
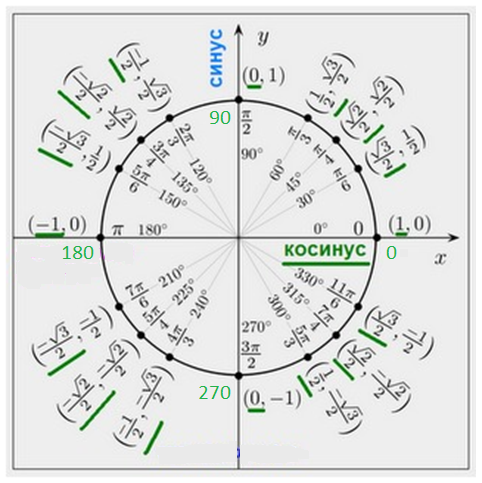



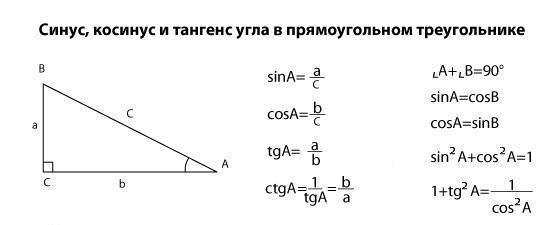

Увеличим или уменьшим треугольник пропорционально, не меняя острый угол. Согласно основному свойству дроби, значения тригонометрических функций угла также останутся неизменными:. Значения тригонометрических функций зависят не от размеров треугольника, а только от градусной меры острого угла. Этот факт позволяет нам расширить понятие тригонометрических функций не только на острые, но и на любые другие произвольные углы — тупые, развернутые. Увеличим или уменьшим прямоугольный треугольник так, чтобы гипотенуза стала равна единице.